404 Brain Not Found
[자료구조] Queue 본문
분류:
- 선형 자료구조
- FIFO(First In First Out) 구조
특징:
- 가장 먼저 들어온 데이터가 가장 먼저 나가는 구조
- 데이터 삽입(enqueue)은 후단(rear)에서, 삭제(dequeue)는 전단(front)에서 이루어짐
- 양쪽 끝에서 데이터의 삽입과 삭제가 일어나므로, 두 개의 포인터(front와 rear)를 사용
- Queue가 비어있는 상태에서 원소를 꺼내려고 하면 'Queue Underflow' 발생
- Queue가 가득 찬 상태에서 원소를 추가하려고 하면 'Queue Overflow' 발생
사용처:
- 프로세스 관리
- 네트워크 패킷 전송 시 버퍼 관리
- 프린터의 출력 처리
- 너비 우선 탐색(BFS) 알고리즘 구현
- 작업 스케줄링
- 메시지 큐 시스템
- 캐시 구현
코드 구현
#pragma once
/*
Queue
*/
template<typename T>
class Queue
{
enum
{
START_ALLOC = 5 // 초기 할당값 10
};
private:
int _capacity; // queue 용량
int _size; // queue 사이즈
int _front; // front Index 데이터의 시작 위치
int _end; // end Index; 데이터가 삽입될 위치
T* _data; // 버퍼
public:
// 생성자
Queue() :_capacity(0), _size(0), _front(0), _end(0), _data(nullptr)
{
Reserve(START_ALLOC);
}
// 소멸자
~Queue()
{
if (_data)
delete[] _data;
}
public:
// 메모리 할당
void Reserve(int newCapacity)
{
T* newData = new T[newCapacity]; // 새로운 버퍼를 할당받는다.
if (_data)
{
// end 인덱스가 front 인덱스보다 작다면 버퍼를 넘어간 케이스
// [][E][][F][]
if (_end <= _front)
{
// front 인덱스부터 배열의 끝부분까지 복사
::memcpy(newData, &_data[_front], (_capacity - _front) * sizeof(T));
// 0번째 인덱스부터 end 인덱스 전 까지 복사
::memcpy(newData, &_data[0], _end * sizeof(T));
// Front Index와 End Index 재지정
// 새로운 메모리로 이동하였으므로, _front는 0번 인덱스가 되고, _end는 _size가 된다.
_front = 0;
_end = _size;
}
// 그렇지 않을 경우 직관적인 Case
// [][F][][][E]
else
{
::memcpy(newData, &_data[_front], (_end - _front) * sizeof(T));
// Front Index와 End Index 재지정
// 새로운 메모리로 이동하였으므로, _front는 0번 인덱스가 되고, _end는 _end - _front가 된다.
_front = 0;
_end = _end - _front;
}
}
_capacity = newCapacity; // capacity 갱신
if (_data) // 이전 버퍼 메모리 할당 해제
delete[] _data;
_data = newData; // 새로 할당받은 버퍼를 가리키도록 갱신
}
// 데이터 추가
void Push(const T& data)
{
// [F/E][0][0][][][]
// F: 데이터의 시작 위치
// E: 데이터가 삽입될 위치
int newSize = _size + 1;
if (_capacity < newSize)
{
int newCapacity = newSize * 1.5;
Reserve(newCapacity);
}
_data[_end] = data;
_end = (_end + 1) % _capacity; // Ring 버퍼를 구현하기 위해서 나머지 연산을 사용한다.
_size = newSize;
}
// 데이터 삭제
void Pop()
{
if (Empty())
{
// data가 없는데 Front를 했다는 것은, Error
throw std::runtime_error("Queue is Empty");
}
_front = (_front + 1) % _capacity; // Ring 버퍼를 구현하기 위해서 나머지 연산을 사용한다.
_size--;
}
// queue의 특징은 넣은 순서대로 데이터가 출력된다
// 선입선출법
const T& Front()
{
if (Empty())
{
// data가 없는데 Front를 했다는 것은, Error
throw std::runtime_error("Queue is Empty");
}
return _data[_front];
}
// queue가 비었는지 확인한다.
bool Empty()
{
if (_size == 0)
return true;
return false;
}
};#include "pch.h"
#include "Queue.h"
int main()
{
Queue<int> q;
for (int i = 0; i < 30; i++)
q.Push(i);
while (!q.Empty())
{
std::cout << q.Front() << " " << std::endl;
q.Pop();
}
// 예상출력값 1,2,3,4
return 0;
}실행 결과

구현 중요 포인트
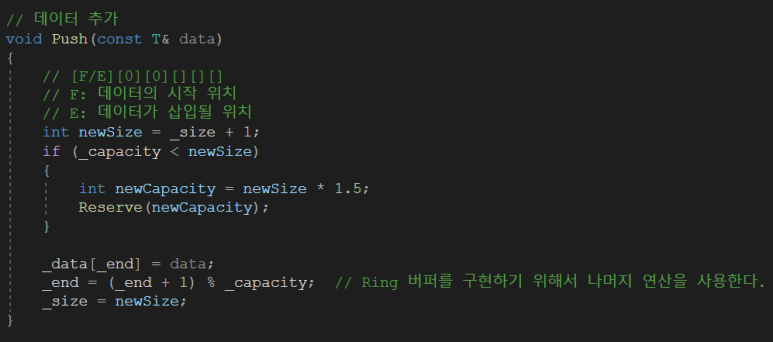
기존 Stack 구현과 마찬가지로, capacity(용량)을 가지고 구현한다. 만약에, 용량이 가득 찼을 경우, 새로운 메모리를 할당받아서 복사시켜줍니다. 하지만 메모리를 복사해 줄 때 주의해야 할 점이 있습니다. Queue는 Ring 버퍼로 구현하기 때문입니다.
Ring Buffer는 말 그대로 도넛 같은 Ring 모양의 Buffer입니다. 기본적으로 프로그래밍 언어에서 배열을 선언하면 메모리 상에서 직선으로 놓이게 됩니다. 그렇기에 시작 위치와 끝 위치를 가지게 됩니다.
그렇기에 일직선에 놓인 배열에서 데이터를 관리하기 위해서는 어쩔 수 없이 데이터를 당기거나(Push) 미는(Pop) 작업이 필요합니다. 하지만 데이터를 밀거나 당기는 것은 for 문을 최소 1차원 이상 돌아야 하기에 O(n) 시간 복잡도를 가지게 됩니다.
그렇기에 사용하는 방식이 링버퍼 방식으로 FrontIndex(시작 인덱스) EndIndex(끝 인덱스)를 가지고 유효 범위를 두고 데이터를 관리하는 것입니다. 배열을 마치 동그란 도넛 모양으로 생각하면 쉽습니다.
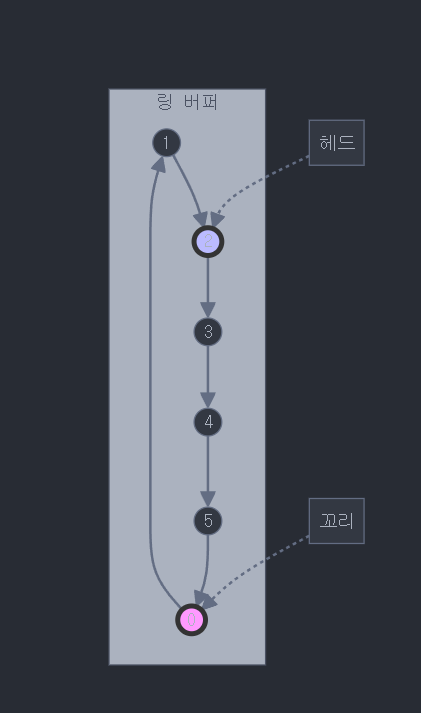
링버퍼를 구현할 때 핵심은 데이터가 추가되어서 배열의 범위를 벗어날 때입니다.
아래의 예시를 보겠습니다. (EndIndex가 배열의 끝부분에 있습니다.)
[][F][][E]
데이터의 시작 위치 1번 인덱스: F
데이터가 삽입될 위치 3번 인덱스: E
이때 데이터가 삽입되면 RingBuffer는 아래의 모습이 돼야 합니다.
[E][F][][]
데이터의 시작 위치 1번 인덱스: F
데이터가 삽입될 위치 0번 인덱스: E
즉 배열의 범위를 넘어가면 나머지 연산을 통하여 반대편 인덱스로 넘어가면 됩니다.
( EndIndex + 1 ) % Capacity

그리고 데이터를 재 할당할 때 RingBuff의 현재 상태에 따라서 복사를 다르게 해야 합니다. 만약에 EndIndex가 FrontIndex보다 작다면, 그것은 EndIndex가 배열의 크기를 초과하여 반대편으로 넘어갔다는 것을 의미하므로, FrontIndex에서 배열의 끝부분까지 복사하고, 0번 인덱스부터 End 인덱스까지 복사합니다. 그렇지 않을 경우는 주석에 써놓은 대로 복사해 주면 됩니다.
'자료구조 > 선형자료구조' 카테고리의 다른 글
| [자료구조] ArrayList (0) | 2024.09.16 |
|---|---|
| [자료구조] Deque (6) | 2024.09.16 |
| [자료구조] Stack (2) | 2024.09.16 |