404 Brain Not Found
[자료구조] HeapTree 본문
분류:
- 비선형 자료구조
- 완전 이진 트리(Complete Binary Tree) 기반
- 우선순위 큐를 위해 고안된 자료구조
특징:
- 부모 노드와 자식 노드 간의 대소 관계가 일정한 완전 이진 트리
- 최대 힙(Max Heap): 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
- 최소 힙(Min Heap): 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
- 중복된 값을 허용
- 배열을 사용하여 효율적으로 구현 가능
- 삽입과 삭제 연산의 시간 복잡도는 O(log n)
- 최대값 또는 최소값을 O(1) 시간에 찾을 수 있음
- 힙 속성(Heap Property)을 유지하기 위해 삽입과 삭제 후 재정렬(heapify) 과정 필요
사용처:
- 우선순위 큐 구현
- 힙 정렬(Heap Sort) 알고리즘
- 운영체제의 작업 스케줄링
- 네트워크 트래픽 제어
- 데이터 압축 알고리즘 (허프만 코딩)
- 다익스트라 알고리즘 등 최단 경로 알고리즘
- 메모리 관리 시스템의 가용 메모리 블록 관리
- 이벤트 드리븐 시뮬레이션
- 중앙값, K번째 큰 값 찾기 등의 문제 해결
#pragma once
#include <vector>
template<typename T>
class HeapTree
{
private:
std::vector<T> _data; // 힙트리 데이터 (이전에 구현했던 ArrayList 사용)
public:
// 생성자
HeapTree()
{
}
// 소멸자
~HeapTree()
{
}
public:
// 힙트리는 데이터를 삽입할때 트리의 가장 리프 노드의 왼쪽부터 채운다.
// 가장 아래 노드부터 부모노드까지, 대소관계를 비교하며 위치를 맞춘다.
void Push(const T& data)
{
_data.push_back(data); // 가장 리프 노드의 왼쪽부터 삽입
int nowIndex = _data.size() - 1; // 현재 인덱스
int parentIndex = (nowIndex - 1) / 2; // 부모의 인덱스
while (parentIndex >= 0 && nowIndex != parentIndex)
{
if (_data[parentIndex] < _data[nowIndex]) // 만약에 현재 인덱스가 부모 인덱스보다 크다면?
{
// 교체 작업을 수행한다.
std::swap(_data[parentIndex], _data[nowIndex]);
nowIndex = parentIndex;
parentIndex = (nowIndex - 1) / 2;
}
else
{
// 부모 노드가 더 크다면 작업을 종료한다.
break;
}
}
}
// 힙 트리 삭제는 부모 노드와 리프 노드의 왼쪽과 자리를 바꾸고, 리프 노드를 삭제한다.
// 부모 노드에서부터 리프노드까지 대소관계를 비교하며 아래로 내려간다.
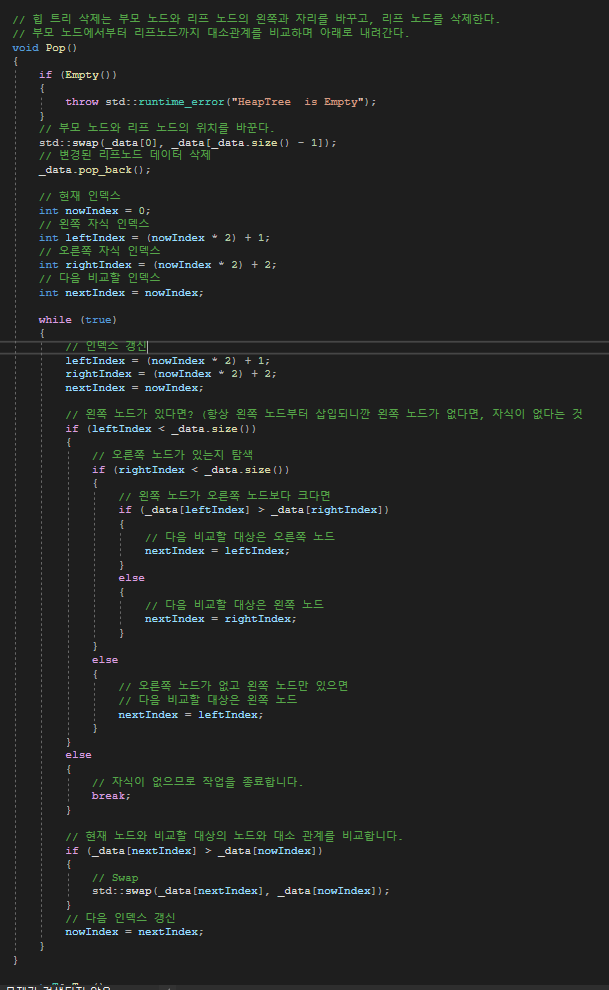
void Pop()
{
if (Empty())
{
throw std::runtime_error("HeapTree is Empty");
}
// 부모 노드와 리프 노드의 위치를 바꾼다.
std::swap(_data[0], _data[_data.size() - 1]);
// 변경된 리프노드 데이터 삭제
_data.pop_back();
// 현재 인덱스
int nowIndex = 0;
// 왼쪽 자식 인덱스
int leftIndex = (nowIndex * 2) + 1;
// 오른쪽 자식 인덱스
int rightIndex = (nowIndex * 2) + 2;
// 다음 비교할 인덱스
int nextIndex = nowIndex;
while (true)
{
// 인덱스 갱신
leftIndex = (nowIndex * 2) + 1;
rightIndex = (nowIndex * 2) + 2;
nextIndex = nowIndex;
// 왼쪽 노드가 있다면? (항상 왼쪽 노드부터 삽입되니깐 왼쪽 노드가 없다면, 자식이 없다는 것
if (leftIndex < _data.size())
{
// 오른쪽 노드가 있는지 탐색
if (rightIndex < _data.size())
{
// 왼쪽 노드가 오른쪽 노드보다 크다면
if (_data[leftIndex] > _data[rightIndex])
{
// 다음 비교할 대상은 오른쪽 노드
nextIndex = leftIndex;
}
else
{
// 다음 비교할 대상은 왼쪽 노드
nextIndex = rightIndex;
}
}
else
{
// 오른쪽 노드가 없고 왼쪽 노드만 있으면
// 다음 비교할 대상은 왼쪽 노드
nextIndex = leftIndex;
}
}
else
{
// 자식이 없으므로 작업을 종료합니다.
break;
}
// 현재 노드와 비교할 대상의 노드와 대소 관계를 비교합니다.
if (_data[nextIndex] > _data[nowIndex])
{
// Swap
std::swap(_data[nextIndex], _data[nowIndex]);
}
// 다음 인덱스 갱신
nowIndex = nextIndex;
}
}
const T& Top()
{
if (Empty())
{
throw std::runtime_error("HeapTree is Empty");
}
return _data[0];
}
bool Empty()
{
return _data.empty();
}
int Size()
{
return _data.size();
}
};#include "pch.h"
#include "HeapTree.h"
int main()
{
HeapTree<int> hp;
hp.Push(3);
hp.Push(1);
hp.Push(4);
hp.Push(20);
hp.Push(13);
hp.Push(5);
hp.Push(6);
hp.Push(8);
hp.Push(999);
hp.Push(14);
hp.Push(12);
while (!hp.Empty())
{
std::cout << hp.Top() << " ";
hp.Pop();
}
return 0;
}
실행 결과

구현 중요 포인트
힙트리를 구현하기 위해서는 힙트리의 성질을 이해해야 합니다.
힙트리는 최대, 최솟값이 트리의 루트에 위치합니다. 이것은 최대, 최소를 빠르게 탐색하기 위하여 설계된 자료구조여서 그렇습니다. 일반적으로 최대, 최소를 찾기 위해서는 O(n)의 시간 복잡도를 가집니다. 하지만 힙 트리의 경우 균형 이진 트리이고, 두 가지 Case로 나누어지므로 O(logN)의 시간 복잡도를 가지게 됩니다.
힙트리의 주요 특성 및 구현
1. 데이터가 삽입될 때 트리의 리프 노드의 왼쪽 자리부터 삽입됩니다.

2. 완벽한 이진 트리의 구조를 이루기 때문에 부모, 자식 인덱스를 계산할 수 있습니다.

3. 데이터가 삽입될 때 리프노드부터 부모 노드까지 대소 관계를 비교하며 최대, 최솟값을 갱신합니다.

4. 데이터가 삭제될 때 부모 노드와 리프 노드 위치를 변경하고 리프노드 삭제 후, 부모 노드에서 리프노드까지 대소 관계를 비교하며 최대, 최솟값을 갱신합니다.
'자료구조 > 비선형자료구조' 카테고리의 다른 글
| [자료구조] BinarySearchTree (C++ 버전, C언어 버전) (4) | 2024.09.16 |
|---|---|
| [자료구조] Graph + 객체지향 다형성 활용 (5) | 2024.09.16 |
| [자료구조] PriorityQueue (1) | 2024.09.16 |