404 Brain Not Found
[자료구조] BinarySearchTree (C++ 버전, C언어 버전) 본문

분류:
- 비선형 자료구조
- 계층적 자료구조
- 이진 트리의 일종
특징:
- 각 노드는 최대 두 개의 자식 노드를 가짐
- 모든 노드에 대해 왼쪽 서브트리의 값 < 노드의 값 < 오른쪽 서브트리의 값
- 중위 순회(In-order traversal)시 정렬된 순서로 노드를 방문
- 평균적인 경우 탐색, 삽입, 삭제 연산의 시간 복잡도는 O(log n)
- 최악의 경우(불균형 트리) 시간 복잡도는 O(n)
- 중복된 키를 허용하지 않음 (일반적인 구현의 경우)
- 트리의 균형이 무너질 경우 성능이 저하될 수 있음
- 자가 균형 이진 탐색 트리(예: AVL 트리, 레드-블랙 트리)는 이를 보완
사용처:
- 데이터베이스 인덱싱
- 심볼 테이블 구현 (컴파일러, 인터프리터)
- 우선순위 큐 구현
- 파일 시스템의 디렉토리 구조
- 검색 엔진의 검색어 자동 완성 기능
- 수학 및 컴퓨터 과학의 집합 ADT(Abstract Data Type) 구현
- 게임 개발에서의 결정 트리
- 허프만 코딩 알고리즘에서 사용
- 키-값 저장 구조 (예: TreeMap in Java)
- 이진 탐색의 동적 버전으로 사용
#pragma once
/*
BinarySearchTree에서 사용할 Node 클래스
*/
template<typename T, typename U>
class Node
{
public:
// 생성자
Node() : parent(nullptr), left(nullptr), right(nullptr) {}
Node(T key, U value) : parent(nullptr), left(nullptr), right(nullptr), key(key), value(value) {}
// 소멸자
~Node() = default;
Node* parent; // 부모 참조
Node* left; // 왼쪽 자식 참조
Node* right; // 오른쪽 자식 참조
T key = {}; // Key 값
U value = {}; // Value 값
};
/*
BinarySearchTree
*/
template<typename T, typename U>
class BinarySearchTree
{
private:
Node<T,U>* _root = nullptr; // Root Node
public:
void Insert(T key, U value); // 데이터 삽입
Node<T, U>* Get(T key); // 데이터 조회
void Remove(T key); // 데이터 제거
void InorderTraversal(); // 중위순회 출력
private:
void Replace(Node<T, U>* u, Node<T, U>* v); // U 노드를 V 노드로 교체
void Remove(Node<T, U>* deleteNode); // 특정 노드 제거
void InorderTraversal(Node<T, U>* node); // 중위순회 출력
};
// 데이터 삽입
template<typename T, typename U>
inline void BinarySearchTree<T, U>::Insert(T key, U value)
{
// 삽입할 데이터로 Node를 만든다.
Node<T,U>* newNode = new Node<T, U>(key,value);
// 루트가 없을경우 첫번째 삽입이 노드가 된다.
if (_root == nullptr)
{
_root = newNode;
return;
}
// Root에서부터 시작
Node<T, U>* node = _root;
// 부모 노드 nullptr
Node<T, U>* parent = nullptr;
// 삽입할 위치 탐색
while (node)
{
// 부모노드 갱신
parent = node;
// 삽입할 Key가 현재 노드보다 크다면
if (key > node->key)
// >>
node = node->right;
else
// 그렇지 않다면 <<
node = node->left;
}
// 새로운 노드 부모 갱신
newNode->parent = parent;
// 맞는 위치에 노드 삽입
if (key > parent->key)
parent->right = newNode;
else
parent->left = newNode;
}
// 데이터 조회
template<typename T, typename U>
inline Node<T,U>* BinarySearchTree<T, U>::Get(T key)
{
// 항상 Root 노드부터 시작
Node<T, U>* node = _root;
// 이진탐색을하여서, 데이터 찾기
while (node)
{
if (key > node->key)
node = node->right;
else if (key < node->key)
node = node->left;
else
{
// 만약에 데이터를 찾았다면 while 문 종료
break;
}
}
// 노드 반환
return node;
}
// 데이터 삭제
template<typename T, typename U>
inline void BinarySearchTree<T, U>::Remove(T key)
{
// 삭제할 노드 조회
Node<T,U>* deleteNode = Get(key);
// 삭제
Remove(deleteNode);
}
template<typename T, typename U>
inline void BinarySearchTree<T, U>::InorderTraversal()
{
InorderTraversal(_root);
}
template<typename T, typename U>
inline void BinarySearchTree<T, U>::InorderTraversal(Node<T, U>* node)
{
if (node)
{
InorderTraversal(node->left);
std::cout << node->key << std::endl;
InorderTraversal(node->right);
}
}
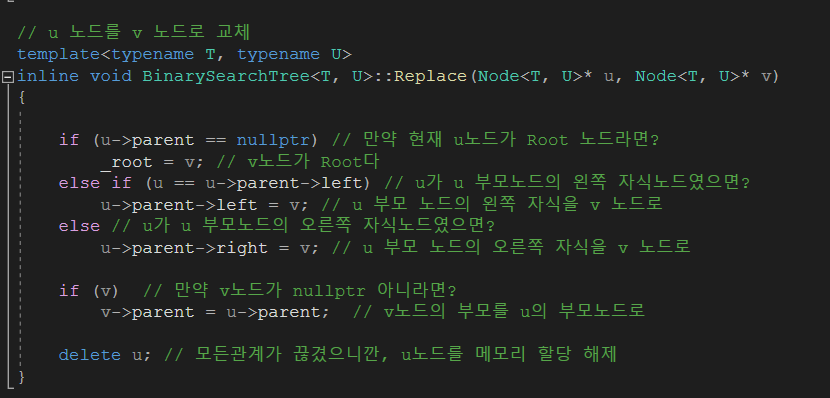
// u 노드를 v 노드로 교체
template<typename T, typename U>
inline void BinarySearchTree<T, U>::Replace(Node<T, U>* u, Node<T, U>* v)
{
if (u->parent == nullptr) // 만약 현재 u노드가 Root 노드라면?
_root = v; // v노드가 Root다
else if (u == u->parent->left) // u가 u 부모노드의 왼쪽 자식노드였으면?
u->parent->left = v; // u 부모 노드의 왼쪽 자식을 v 노드로
else // u가 u 부모노드의 오른쪽 자식노드였으면?
u->parent->right = v; // u 부모 노드의 오른쪽 자식을 v 노드로
if (v) // 만약 v노드가 nullptr 아니라면?
v->parent = u->parent; // v노드의 부모를 u의 부모노드로
delete u; // 모든관계가 끊겼으니깐, u노드를 메모리 할당 해제
}
template<typename T, typename U>
inline void BinarySearchTree<T, U>::Remove(Node<T, U>* deleteNode)
{
if (deleteNode == nullptr) return;
if (deleteNode->left == nullptr) // 삭제할 노드의 왼쪽 노드가 없다면?
Replace(deleteNode, deleteNode->right); // 오른쪽 자식노드와 교체
else if (deleteNode->right == nullptr) // 삭제할 노드의 오른쪽 노드가 없다면?
Replace(deleteNode, deleteNode->left); // 왼쪽 자식노드와 교체
else
{
Node<T, U>* nextNode = nullptr;
// 오른쪽 자식 노드가 있다면, 오른쪽 자식 노드의 가장 왼쪽 노드가 다음 노드
if (deleteNode->right)
{
Node<T, U>* parent = deleteNode->right;
Node<T, U>* node = parent->left;
while (node)
{
parent = node;
node = parent->left;
}
nextNode = parent;
}
// 오른쪽 자식노드가 없다면,
// 부모노드를 탐색하여서 삭제할 노드의 부모 노드가 왼쪽 자식일때를 찾는다. (말이 좀 어렵다)
else
{
Node<T, U>* parent = deleteNode->parent;
Node<T, U>* node = deleteNode;
while (parent && parent->right == node)
{
node = parent;
parent = parent->parent;
}
nextNode = parent;
}
// 값 바꿔치기
deleteNode->key = nextNode->key;
deleteNode->value = nextNode->value;
// 실제 삭제할 노드를 삭제 (재귀 호출)
Remove(nextNode);
}
}#include "pch.h"
#include "BinarySearchTree.h"
int main()
{
BinarySearchTree<int, char> bst;
bst.Insert(20, 'A');
bst.Insert(10, 'B');
bst.Insert(30, 'C');
bst.Insert(25, 'C');
bst.Insert(40, 'C');
bst.Insert(26, 'C');
bst.Insert(50, 'C');
// bst.InorderTraversal();
bst.Remove(20);
bst.InorderTraversal();
return 0;
}
실행 결과

구현 중요 포인트
이진 탐색 트리 (Binary-Search-Tree)는 이진탐색을 기반으로 만들어진 자료구조 입니다. 검색에 굉장히 장점이 있는 자료구조이며, 트리의 균형을 완벽하게 이루고 있다면, 검색할때 O(logN) 시간 복잡도를 가집니다. 그 이유는 검색을 할때 무조건 2가지 Case로 나누어지기 때문입니다.
하지만 트리의 균형이 깨지면, 검색을 할때 최대 시간복잡도가 O(N)이 걸릴 수 있기 때문에 나중에 구현해볼 AVL 트리와 Red-Black-Tree에서는 알고리즘을 통하여 데이터를 삽입하거나 삭제할때 자동으로 균형을 맞추게 됩니다.
먼저 BinarySearchTree는 Node 기반으로 구현을 하였습니다.
또한 Parent 노드를 참조하도록 설계하였습니다.
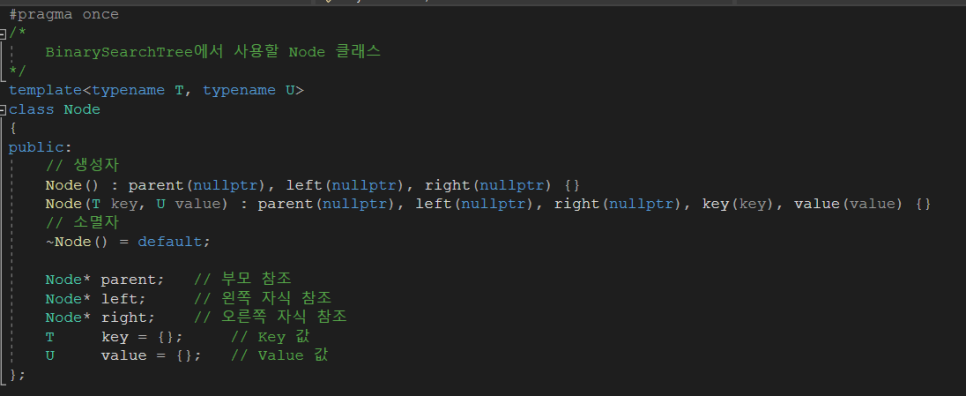
BinarySearchTree에서 삽입, 삭제, 검색 3가지만 구현하였습니다.
그리고 BST가 잘 구현이 되었는지 확인을 하기 위하여 중위순회 알고리즘을 추가하였습니다.

데이터 삽입 로직입니다.
이진탐색을하여서 데이터가 삽입될 위치에 찾아가서 삽입해줍니다. 비교적 삽입 연산은 간단합니다.
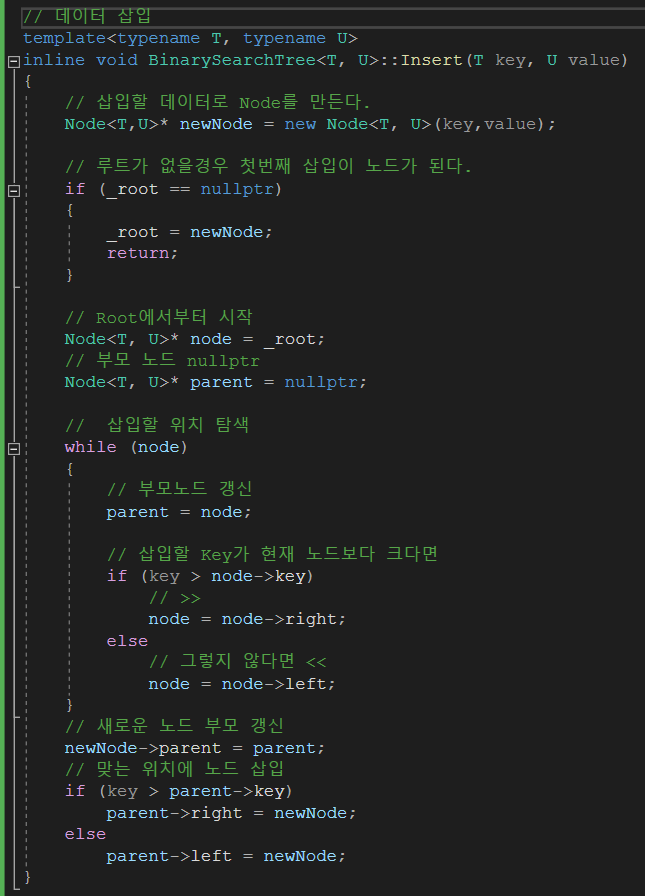
다음은 삽입한 데이터를 조회하는 로직입니다.
이진탐색을 하여서 데이터를 찾습니다.

다음은 데이터 삭제 로직입니다.
Get 메소드를 이용하여 삭제할 Node를 찾고 Remove (오버로딩된) 함수를 호출합니다.

오버로딩된 Remove 함수는 노드의 자식 Case를 분류하여서 삭제를 진행합니다.
이때 Replace 메소드를 호출하는데, 현재 노드가 parent, left, right 3가지 참조를 사용합니다.
이때 참조를 끊고, 맺는 로직이 반복되기 때문에 Replace 함수를 따로 만들어서 사용했습니다.

두개의 노드를 Swap 하는 Replace 함수 입니다.
마지막으로 테스트를 하기위하여 중위순회 알고리즘을 구현하였습니다.

그리고 기존에 C언어로 구현한 BST가 있어서, C언어로 구현한 BST 코드도 올리겠습니다.
해당 버전은 Parent를 참조하지 않고, 재귀로직을 최대한 이용하여서 구현한 BST 입니다.
#pragma once
#include <stdio.h>
#include <stdlib.h>
struct Node {
int key;
int data;
struct Node* left;
struct Node* right;
} typedef Node;
void Insert(Node** node, int key, int data);
int Get(Node* root, int key);
void Delete(Node** root, int key);
void SearchAll(Node* node);
Node* _Insert(Node* node, Node* insertNode);
Node* _Get(Node* node, int key);
Node* _Delete(Node* node, int key);
Node* _DeleteMin(Node* node, Node* minNode);
#include "binarySearchTree.h"
#include <string.h>
void Insert(Node** node, int key, int data) {
// Node* newNode = (Node*)malloc(sizeof(Node));
Node newNode;
newNode.data = data;
newNode.key = key;
newNode.left = NULL;
newNode.right = NULL;
*node = _Insert((*node), &newNode);
}
Node* _Insert(Node* node, Node* insertNode) {
if (node == NULL) {
// 기존 return insertNode;
// 실제로 데이터가 추가되었을때 메모리를 할당받고 복사해줌
Node* newNode = (Node*)malloc(sizeof(Node));
memcpy(newNode, insertNode, sizeof(Node));
return newNode;
}
if (insertNode->key > node->key) {
node->right = _Insert(node->right, insertNode);
}
else if (insertNode->key < node->key) {
node->left = _Insert(node->left, insertNode);
}
else {
node->data = insertNode->data;
}
return node;
}
int Get(Node* root, int key) {
Node* findNode = _Get(root, key);
if (findNode == NULL) {
return -1;
}
return findNode->data;
}
Node* _Get(Node* node, int key) {
if (node == NULL) {
return NULL;
}
if (key > node->key) {
return _Get(node->right, key);
}
else if (key < node->key) {
return _Get(node->left, key);
}
else {
return node;
}
return 0;
}
void Delete(Node** root, int key) {
*root = _Delete(*root, key);
}
Node* _Delete(Node* node, int key) {
if (node == NULL) {
return NULL;
}
if (key > node->key) {
node->right = _Delete(node->right, key);
}
else if (key < node->key) {
node->left = _Delete(node->left, key);
}
else {
if (node->left == NULL && node->right == NULL) {
free(node);
return NULL;
}
else if (node->left == NULL) {
Node* retNode = node->right;
free(node);
return retNode;
}
else if (node->right == NULL) {
Node* retNode = node->left;
free(node);
return retNode;
}
else {
Node* swapNode;
node->right = _DeleteMin(node->right, &swapNode);
swapNode->left = node->left;
swapNode->right = node->right;
free(node);
return swapNode;
}
}
return node;
}
Node* _DeleteMin(Node* node, Node** minNode) {
if (node->left == NULL) {
*minNode = node;
if (node->right != NULL) {
return node->right;
}
return NULL;
}
return node->left = _DeleteMin(node->left, minNode);
}
void SearchAll(Node* node) {
if (node == NULL) {
return;
}
SearchAll(node->left);
printf("%d ", node->key);
SearchAll(node->right);
}
'자료구조 > 비선형자료구조' 카테고리의 다른 글
| [자료구조] Graph + 객체지향 다형성 활용 (5) | 2024.09.16 |
|---|---|
| [자료구조] PriorityQueue (1) | 2024.09.16 |
| [자료구조] HeapTree (1) | 2024.09.16 |