404 Brain Not Found
[자료구조] Graph + 객체지향 다형성 활용 본문
분류:
- 비선형 자료구조
- 노드(정점)와 엣지(간선)로 구성된 자료구조
특징:
- 노드(Vertex)와 노드 간의 관계를 나타내는 엣지(Edge)로 구성
- 방향 그래프(Directed Graph)와 무방향 그래프(Undirected Graph)로 구분
- 가중치 그래프(Weighted Graph)와 비가중치 그래프로 구분
- 순환(Cycle)이 있을 수 있음
- 연결 그래프(Connected Graph)와 비연결 그래프로 구분
- 인접 행렬(Adjacency Matrix) 또는 인접 리스트(Adjacency List)로 표현 가능
- 트리는 그래프의 특수한 형태
- 노드 간의 경로(Path)와 거리(Distance) 개념 존재
- 탐색 알고리즘: 깊이 우선 탐색(DFS), 너비 우선 탐색(BFS) 등
사용처:
- 소셜 네트워크 분석 및 모델링
- 지도 및 내비게이션 시스템 (도로 네트워크 표현)
- 컴퓨터 네트워크 토폴로지 설계 및 분석
- 웹 페이지 간의 링크 구조 표현 (검색 엔진 알고리즘)
- 추천 시스템 (사용자-아이템 관계 모델링)
- 생물학적 네트워크 (단백질 상호작용 네트워크 등)
- 작업 스케줄링 (작업 간 의존성 표현)
- 컴파일러의 제어 흐름 그래프
- 전기 회로 설계 및 분석
- 게임 개발 (레벨 디자인, AI 경로 찾기 등)
#pragma once
#include <unordered_map>
#include <functional>
#include <stdexcept>
#include <vector>
/*
Pos
*/
struct Pos
{
public:
int x;
int y;
Pos(int x, int y) : x(x), y(y) {}
bool operator==(const Pos& other) const
{
return x == other.x && y == other.y;
}
};
// std::hash 특수화
namespace std {
template <>
struct hash<Pos> // Pos 타입에 대해 특별히 정의된 Hash 함수를 제공한다.
{
size_t operator()(const Pos& p) const
{
// 1. p.x의 해시값 계산
// 2. p.y의 해시값을 계산하고 왼쪽으로 시프트 연산
// 3. 두 연산 결과를 XOR 연산하여 최종 해시값 생성
return hash<int>()(p.x) ^ (hash<int>()(p.y) << 1);
}
};
}
/*
Graph
그래프 최상위 부모 클래스
*/
class Graph
{
protected:
size_t _size;
public:
// explicit 암시적 형변환을 막는 키워드 (나중에 C++ 문법 강의에서 다뤄볼 에정)
explicit Graph(size_t size) : _size(size) {}
// 소멸자
virtual ~Graph() = default;
// AddEdge 간선 추가
virtual void AddEdge(int from, int to) = 0;
// HasEdge 간선이 연결되어있는지 반환
virtual bool HasEdge(int from, int to) const = 0;
};
/*
AdjacencyMatrix
인접 행렬 (2차원 배열 버전)
최대 10000개의 데이터를 저장 가능,
10000개 이상부터는 메모리를 많이 차지한다고 판단하기에,
HashMap으로 구현된 인접행렬 사용
*/
class AdjacencyMatrix : public Graph
{
private:
bool _matrix[1000][1000]; // 10,000개의 데이터를 저장할 수 있다.
public:
// 생성시, _matrix 값을 모두 false로 밀어버린다.
explicit AdjacencyMatrix(size_t size) : Graph(size)
{
std::memset(_matrix, 0, sizeof(_matrix));
}
// 간선 추가
void AddEdge(int from, int to) override
{
if (from < 0 || to < 0 || from >= _size || to >= _size)
{
throw std::out_of_range("AdjacencyMatrix: Index out of range");
}
_matrix[from][to] = true;
_matrix[to][from] = true; // 양방향 그래프
}
// 간선 체크
bool HasEdge(int from, int to) const override
{
if (from < 0 || to < 0 || from >= _size || to >= _size)
{
throw std::out_of_range("AdjacencyMatrix: Index out of range");
}
return _matrix[from][to];
}
};
/*
AdjacencyMatrixHash
인접 행렬 (해시 버전)
10,000개 이상의 정보를 표현할 수 있다.
*/
class AdjacencyMatrixHash : public Graph
{
private:
std::unordered_map<Pos, bool> _matrixHashMap;
public:
explicit AdjacencyMatrixHash(size_t size) : Graph(size) {}
void AddEdge(int from, int to) override
{
if (from < 0 || to < 0 || from >= _size || to >= _size)
{
throw std::out_of_range("AdjacencyMatrixHash: Index out of range");
}
_matrixHashMap[Pos{ from, to }] = true;
_matrixHashMap[Pos{ to, from }] = true; // 양방향 그래프
}
bool HasEdge(int from, int to) const override
{
if (from < 0 || to < 0 || from >= _size || to >= _size)
{
throw std::out_of_range("AdjacencyMatrixHash: Index out of range");
}
return _matrixHashMap.count(Pos{ from, to }) > 0;
}
};
/*
AdjacencyList
인접 리스트
*/
class AdjacencyList : public Graph
{
private:
std::vector<std::vector<int>> _adjacencyList;
public:
explicit AdjacencyList(size_t size) : Graph(size)
{
_adjacencyList.resize(size);
}
void AddEdge(int from, int to) override
{
if (from < 0 || to < 0 || from >= _size || to >= _size)
{
throw std::out_of_range("AdjacencyList: Index out of range");
}
_adjacencyList[from].push_back(to);
_adjacencyList[to].push_back(from); // 양방향 그래프를 위한 추가
}
bool HasEdge(int from, int to) const override
{
if (from < 0 || to < 0 || from >= _size || to >= _size)
{
throw std::out_of_range("AdjacencyList: Index out of range");
}
return std::find(_adjacencyList[from].begin(), _adjacencyList[from].end(), to) != _adjacencyList[from].end();
}
};
위의 그래프를 기준으로 그래프를 만들어보겠습니다. ( 일단은 가중치를 생각하지 않겠습니다. )
그리고 그래프를 탐색하기 위하여 DFS 알고리즘을 이용하여 탐색하겠습니다.
DFS 알고리즘에 대한 설명은 해당 포스트에서 하지 않겠습니다. 나중에 알고리즘 내용을 다룰때 설명하겠습니다.
#include "pch.h"
#include "Graph.h"
#include <vector>
#include "Queue.h"
std::vector<int> vertexList = {0,1,2,3,4,5,6};
bool discoverd[7] = {false,};
void DFS(int from, const Graph& g, Queue<int>& q, int dest, bool& end)
{
for (const auto& to : vertexList)
{
if (discoverd[to])
continue;
if (g.HasEdge(from, to))
{
discoverd[to] = true;
q.Push(to);
if (to == dest)
{
end = true;
return;
}
DFS(to,g,q, dest, end);
if (end)
return;
}
}
}
int main()
{
{
// 인접 행렬 2차원 배열 사용
AdjacencyMatrix graph(100);
graph.AddEdge(0, 1);
graph.AddEdge(1, 2);
graph.AddEdge(1, 3);
graph.AddEdge(3, 4);
graph.AddEdge(3, 5);
graph.AddEdge(2, 6);
graph.AddEdge(2, 5);
Queue<int> path;
path.Push(0);
discoverd[0] = true;
bool end = false;
DFS(0, graph, path, 5, end);
while (!path.Empty())
{
std::cout << path.Front() << " -> ";
path.Pop();
}
std::cout << "End" << std::endl;
}
{
// 인접 행렬 Hash 사용
AdjacencyMatrixHash graph(100);
graph.AddEdge(0, 1);
graph.AddEdge(1, 2);
graph.AddEdge(1, 3);
graph.AddEdge(3, 4);
graph.AddEdge(3, 5);
graph.AddEdge(2, 6);
graph.AddEdge(2, 5);
Queue<int> path;
path.Push(0);
discoverd[0] = true;
bool end = false;
DFS(0, graph, path, 5, end);
while (!path.Empty())
{
std::cout << path.Front() << " -> ";
path.Pop();
}
std::cout << "End" << std::endl;
}
{
// 인접 리스트 사용
AdjacencyList graph(100);
graph.AddEdge(0, 1);
graph.AddEdge(1, 2);
graph.AddEdge(1, 3);
graph.AddEdge(3, 4);
graph.AddEdge(3, 5);
graph.AddEdge(2, 6);
graph.AddEdge(2, 5);
Queue<int> path;
path.Push(0);
discoverd[0] = true;
bool end = false;
DFS(0, graph, path, 5, end);
while (!path.Empty())
{
std::cout << path.Front() << " -> ";
path.Pop();
}
std::cout << "End" << std::endl;
}
return 0;
}실행 결과
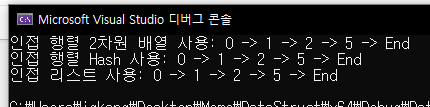
구현 중요 포인트
우선, 3가지의 그래프를 구현할것이기 때문에 추상화를 사용하여 다형성을 활용하려고 했습니다.
최상위에 Graph 클래스를 만들고 AddEdge, HasEdge 두개의 추상 메소드를 사용하여 구현하였습니다.
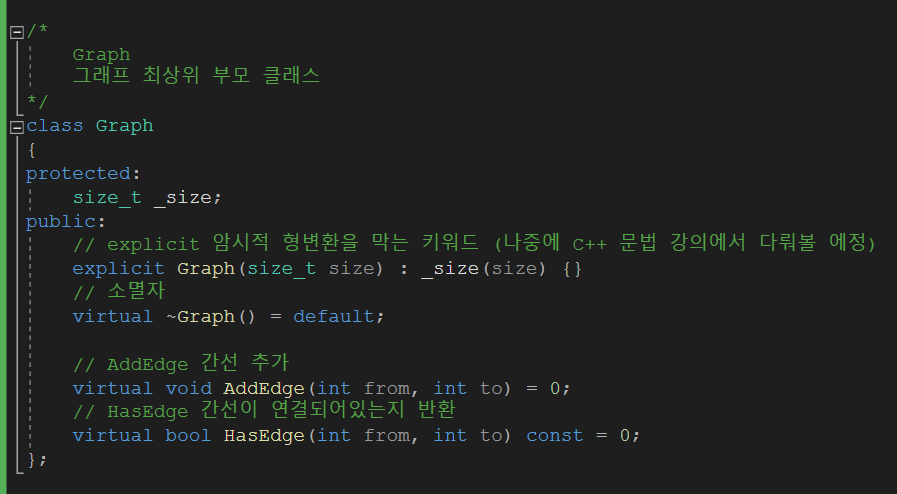
메소드의 매개변수는 똑같기 때문에 사용하는 쪽에서는 해당 클래스가 무엇인지 내부적으로 어떻게 동작하는지 이해할 필요가 없습니다.
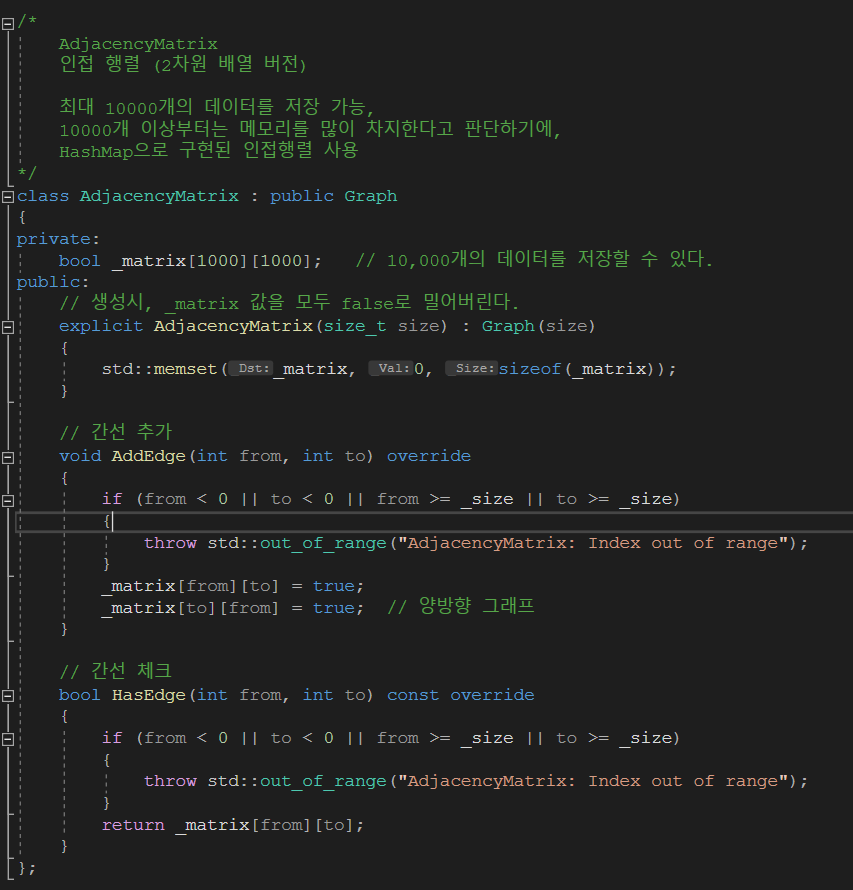
인접 행렬 (2차원 배열 버전)은 최대 10,000개의 데이터를 저장 가능하도록 구현하였습니다. 그래프를 양방향으로 설정하였습니다.

인접 행렬(Hash)의 경우는 대용량의 데이터를 그래프로 표현할 수 있게 해주었습니다. unordered_map은 C++에서 HashMap입니다. 그리고 Key값을 Class로 구현하였기 때문에 Hash에 필요한 연산자를 오버로딩 해주어야 합니다.

== 연산자와, Pos 클래스의 hash값을 확장해주어야 합니다.
나중에 Hash의 자료구조에 대해서 다루면 좀 더 이해하기 쉬울 것 입니다.
이제 테스트 코드를 작성하겠습니다.
테스트는 DFS 알고리즘을 사용하여 구현하였습니다.
Start: 출발 지점에서 Dest: 목적지점까지 경로를 출력해주는 테스트 입니다.

인접행렬 (2차원 배열), 인접행렬 (HashMap), 인접리스트 3가지 모두 Graph 클래스를 추상화한 클래스이기에 사용하는 코드는 모두 똑같습니다. 이것이 객체지향의 강력한 장점 입니다
'자료구조 > 비선형자료구조' 카테고리의 다른 글
| [자료구조] BinarySearchTree (C++ 버전, C언어 버전) (4) | 2024.09.16 |
|---|---|
| [자료구조] PriorityQueue (1) | 2024.09.16 |
| [자료구조] HeapTree (1) | 2024.09.16 |